磁北線を引くためのプログラム for MSX-BASIC

磁北線とは

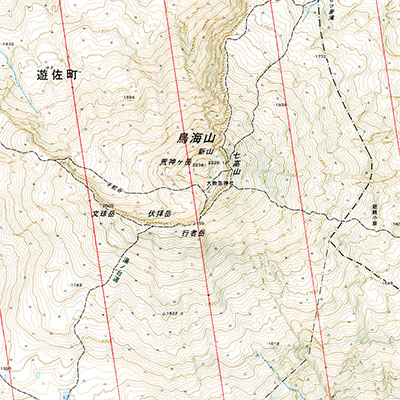
赤い線が磁北線。市販されている地形図には表記されていないので、後から自分で引く必要がある。

　登山には欠かせない国土地理院の地形図。地形図が示す北(真北)と、方位磁針が指す北(磁北)は、一致しないことがよく知られています。方位磁針が示す北は北極点ではなく、そこから若干ずれた場所にあります。そのため、方位磁針を使って地図を見る時には、このズレを補正してやる必要があります。その際、真北に対して磁北がどれくらいズレているかを示す線、つまり磁北の方向を示す線を引いておくと何かと便利です。この線を「磁北線」と呼びます。

磁北線を引こう

　真北に対する磁北のズレは、角度で表されます。2万5000分の１地形図の場合、凡例のところに「西偏角度」の表記があります。
　磁北線を引く場合、分度器でこの角度を測るのが最も手っ取り早いでしょう。しかし三角関数を使えば、分度器なしで正確なプロットが可能です。ここではMSX-BASIC上で、三角関数を使って磁北線を引くためのプログラムを作ってみます。

分度器なしでも正確に引ける理屈

　なぜ三角関数で磁北線が引けるのか。その仕組みを浚ってみましょう。
　地形図の図郭の長さは決まっています。現行の1/25000地形図の場合、南北方向の長さは約42cmあります(実際の距離では約10.5kmに相当します)。この地図の東端を底辺とした場合、磁北線は南東端を頂点とする直角三角形の斜辺であると見なすことができます。斜辺と底辺の内角が西偏角度である直角三角形をプロットすれば、磁北線が引けるということですな。

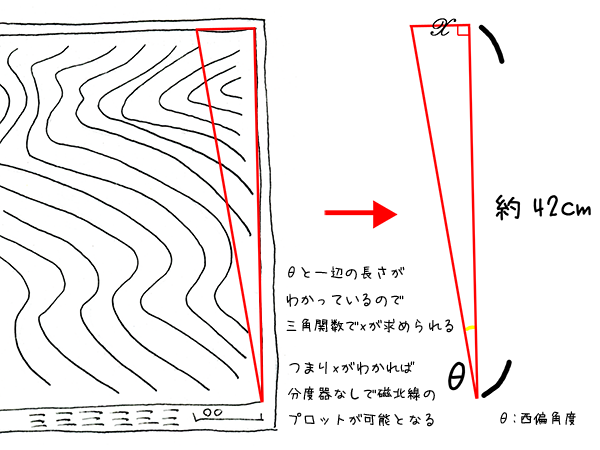
　そのためには、残る一辺の長さを求める必要があります。そこで出てくるのが三角関数tanです。
　底辺ひとつの長さと、頂点の角度はすでに判明しています。ですので残る一辺の長さはtanによる以下の計算式で求められます。

　これをプログラムに置き換えれば、西偏角度を入力するだけで、その角度を斜辺とする直角三角形を描くために必要な、残る一辺の長さがわかるという仕組みです。求めた辺の長さをxとした場合、地図の北東端から西にx cm離れたところと南東端を結べば、それが磁北線となります。

換算が必要だ！

　三角関数を使って磁北線を引く方法はわかりました。しかしプログラムにする場合、そう単純にはいきません。なぜなら二つ問題があるからです。ひとつはMSX-BASICの三角関数は、角度(度数法)をラジアン(弧度法)で与える仕様であること。もうひとつは、地形図に記載された西偏角度が度分秒(六十進法)であるのに対し、MSX-BASICの三角関数は十進法で数値を扱っていることです。
　たとえば西偏角度が8°10’の場合、MSXに直接「PRINT TAN(8.10)」と入力すると、8度10分の正接ではなく、8.1ラジアンの正接が返ってきます。さらに言うと8.10は8度10分ではなく、8.1°なので、やはり正確な数値とはなりません。
　ですので、計算や結果表示の際には、単位を換算してやらねばなりません。換算しないと、正確な磁北線が引けません。正確でなければ地図読みに影響が出てしまいますので、わりと由々しき問題です。

　度数法と弧度法の変換は以下の計算式で可能です。

　度分秒(○度△分×秒)を十進数(○.□度)に変換するにはまず、度の部分と、分以下の部分を分けなければなりません。六十進法でカウントしているのが分以下の部分だからです。
　分離には割り算を使います。入力した数値を100倍して、100で割った商が度、その余りが分といった具合です。100倍するのは、分の部分を整数化した方が計算しやすいため。西偏角度は分までが表記されています。つまり2桁を整数化すればよいので、100倍すれば済むという理屈です。
　分を十進数に置き換えるには、「1度(=60分)のうちに占める割合」を求めます。数式で表すと以下のとおりです。

　yはすでに100倍してあります。本来の数値はその1/100ですので、分子の100は相殺されます。ですのでさきほどの余りを60で割れば、求める数値が得られます。
　分を十進数に置き換えたら、それをさきほど度の部分に加算して、度分秒の換算は完了です。

あとは計算するだけ〜使い方

　これで準備は整いました。以上の手順に従って、MSX-BASIC用のプログラムを書くと以下のようなかんじです。精度を考慮して、数値は倍精度で扱っています。

　60行から70行が、入力した角度を10進法に変換する処理です。80行、TAN関数の引数部分のR*Dが、ラジアンへの変換処理です。その準備として、40行で1°あたりのラジアンこと、円周率を180で割った数値を変数Rとして定義しています。

　使い方は、数値を入力するだけ。実行すると西偏角度を訊いてきます。地形図記載の角度を入力してください。度と分の部分は小数点で区切ってください。分は一の位も省略せず、二桁分入力してください。
　入力すると、その角度をプロットするのに必要な辺の長さ(単位・cm)が返ってきます。地図の北東端から左、求めた長さのところから、南東端に向かって直線を引けば、それが磁北線となります。その際60cmほどの定規があると便利でしょう。一本磁北線を引いたら、それと平行する線を次々に引いていけば、地図全体に磁北線をプロットできます。

　少し手を加えれば、西偏角度に応じた辺の長さを一覧表にして表示することもできるでしょう。しかしこれで当座の用は足りるので、これでおわりにしときます(おい)。

変数表

R:1°あたりのラジアン(円周率/180)
D:西偏角度
T:西偏角度の正接
L:図郭の長さ(42cm)
HP:西偏角度の整数部分
TP:西偏角度の分秒部分